I put off translating this note of Franco’s because every time I looked at it in Italian, I couldn’t follow the argument. If I couldn’t follow it, how could I translate it? Not only that, it would be a great personal embarrassment to me to get it wrong. It is a matter of solving what we used to call in middle school (junior high school, we called it) a “story problem”. I used to be good at such things. If these days I can’t even follow the solution to a problem in simple arithmetic, what does that say about the state of deterioration of my brain?
However one of the participants on Tarot History Forum urged me to do it (viewtopic.php?f=11&t=1100#p18158), so I took the plunge. After many hours of puzzling over it, I concluded that Franco was incorrect in his solution the arithmetic problem that he formulated. So after the translation, at the risk of further embarrassment, I posted my critique, which I include here as well.
Below, in the translation, the comments in brackets are by me, and the page numbers correspond to those of the original, "1477: Bologna – Aritmetica per carte e trionfi", at http://www.naibi.net/A/323-BONOZZI-Z.pdf, originally put online June 9, 2014.
I originally posted my translation on Dec. 3, 2016, at http://forum.tarothistory.com/viewtopic.php?f=11&t=1128#p18214, after which in the next post is my critique of the argument, posted the same day. After reading it Franco emailed me to say
After my critique, in response to a continuing request for translations relative to the issue, I posted translations of the 1908 discussion by the Italian scholar Orioli and of the original contract of 1477 as published by him. This current blog post ends with these translations.In this particular case, I am somewhat glad to have been found to be wrong. Indeed, the year 1477 appeared too late for a 5x14 or a similar pack, and it could probably only be coherent with some unknown local habit.
1477 Bologna: Arithmetic for cards and triumphs
Franco Pratesi – 09.06.2014
Introduction
The idea for writing this note comes from rereading an article published more than a century ago, which directed attention, among other things, to an important Bolognese document of 1477. (1) A copy of the original article with some comments is even available on the Internet. (2) It is a well known text variously commented on by several experts. Some deductions derived from that information seem to have to be revised; others are better understood with a different assessment; others seem to me would require further thought and reflection.
The justification for submitting these reflections to the attention of the experts is that ultimately I have provided many new numbers for card games that should be granted to me from reasoning a bit on the old numbers supplied by others.
The Data
The earliest documents found in the archives of Bologna and published by Orioli represented very early evidence, such as to lead many experts to consider Bologna a very important center for the production of playing cards, beginning from their first diffusion. It is not easy to judge if such a conclusion is due to the fact that similar documentation in other cities and for previous periods. had not yet been found
But if we consider that the use of playing cards was already common for some time (for example in Florence at least from the beginning of 1377, so much so that the councilors concerned were induced to prohibit its further spread), the possible Bologna priority is reduced at most to the use of the woodcut as an important part of the production.
German card makers
From the point of view of woodcuts, still more significant is the large presence of German card makers among those documented in Bologna. It is known that the craft of woodworking for reproduction of pictures was very advanced in the regions of central and southern Germany and adjacent areas. It seems that all the oldest woodcuts that have come down to us stem from one area or another of so-called Mitteleuropa.
At this point it seems to me that the question is reduced to one alternative for resolution: did German playing card makers export to the rich Italian cities the production of playing cards or did they just flock to Italy because a production already widespread could take advantage of their technical expertise in woodworking?
Here the date becomes decisive, which is old only only in relation to others noted, but not so much as to suggest the introduction of new and original items. In my view the same phenomenon happened with playing cards as occurred with the manufacture of shoes: German shoemakers were very capable and easily found a new and abundant clientele in Italy, (3) but it is not legitimate to draw the consequence that in our cities shoes were introduced by German shoemakers.
Naibi in Florence
Even before woodcuts and the Florentines’ use of naibi and cards, the way appears to have been prepared with drawing and painting on pieces of parchment. In this regard, in the article in question we read a cursed affirmation:
Naibi. E questa stessa parola si trova spesso ricordata sul principio del secolo XV in atti notarili fiorentini, dove si descrivono le carte quali foglietti in pergamena artisticamente figurati e dipinti.2
(Naibi. And this same word is often mentioned, in the beginning of the 15th century, in Florentine notary acts, which describe cards as sheets of parchment, artistically depicted and painted.)
I do not know Orioli’s reliability, but I have seen that the archives that he frequented were Bolognese and not Florentine. I do not think he spent much time in Florentine archives; perhaps the only important news stemmed only from word of mouth among archivists of the era.
Twenty years ago I wrote in this regard: (4)
Since then I have flipped through some other notarial registers, but without finding anything in the archival collection; better to turn to Bologna, for now.If it were possible to document that claim with specific references, related in particular to the end of the fourteenth century, one would have a very useful confirmation of the value of this type of naibi. Unfortunately, the number of Notarial codices in the Pre-cosimian Archives is so high that it is virtually impossible to examine them in a comprehensive manner. Furthermore, the notarial writing of the time is much trickier to decipher than those prevailing in other documents, and my reading ability is often insufficient. It is therefore no wonder if the examination of a small sample of notarial codices of the fourteenth century (where one must also have been able to find some citations of naibi in the years immediately preceding 1377) provided a disappointing result: I found there a few inventories of goods and none that contained naibi.
The numbers of cards and of triumphs
This is precisely the point that is making me revisit the subject after a long time. I remembered well the fundamental concept of this document published by Orioli, a contract of Peter Bonozzi of Bologna, with whom he undertook in 1477 to secure his son, a card maker, a commitment to produce cards and triumphs exclusively for the client Roberto di Blanchelli under precise conditions.
Of the figures reported then, in 1908, one can get more related important information, as follows.
- 1) both cards and triumphs were used for playing [giocare];
2) cards were only 40, triumphs 60;
3a) production occurred in groups of 125 decks of cards, or in the case of a smaller number of groups also including packs of triumphs, in an "equivalent" manner, ie, with a same total number of cards.
3b) each card, whether belonging to cards or triumphs, required roughly the same commitment to work and the same raw materials, so that differences in price thus did not exist (a rasone de carta per carta debba essere pagato come de le carte e non più [because card for card should be paid as cards and no more].)
We will start precisely from the number registered with accuracy: 125 decks of cards. This is the only number given for the quantity of cards in the old document, published for the first time in 1908; Orioli inserted the others in 1908 on his own initiative.
Personally, I have always found, for various periods, that the manufacture and sale of playing cards was made taking as a unit a dozen decks. Indeed, they usually had exact figures, i.e. expressed in whole numbers of lire, only for dozens of packs, while the price of a single pack had to be expressed using all the small change available after lire, namely either soldi, a twentieth of a lire, or denari, twelfths of a soldo
3
In short, if this document had read, instead of 125, a number of 120 decks, I would be more at ease, and even more if I had found 144, a dozen dozens, one gross.
Despite everything, this number 125 must be accepted, and indeed will be taken as a fixed point of departure for further calculations. There remains only a certain underlying skepticism about why that precise number of decks was chosen as the basis of this production contract.
The fundamental question which confronts us now is as follows. If instead of producing cards they produced triumphs, how many decks of triumphs corresponded to 125 decks of cards?
With the elements available, it is an elementary school arithmetic problem that would only have the difficulty for the pupil of giving as its solution a fractional number of packs, which is not very nice in any elementary school.
Orioli in fact tells us that the cards were 40 and triumphs 60 and the poor student is thus finds that to 125 decks of cards correspond approximately 83.33 decks of triumphs; to have a more accurate result one would have made oneself familiar beforehand with the numbers of the period (also themselves poorly suited to counting playing cards).
It must, however, be noted that we are using numbers from different sources: the number 125 is of
1477, the numbers 40 and 60 are of 1908! Not to say that the integers are transformed over the years, but only that the problem would be proposed more correctly if all three numbers were taken from 1477 and the same author.
Instead, the original contract tells us precisely nothing about the number of cards in the common deck, or of that of triumphs; it tells us only that the two numbers were different and makes us understand clearly that the number of triumphs was greater than that of cards, but does not specify the difference.
Everything here can be verified in the passage in question, copied as follows.
Now it's up to us to reconstruct the situation and re-propose the problem in terms as correct as possible, or at least convincing. The trouble is that great uncertainty is encountered in the possible data.Item che el prefato ser Roberto sia obligato dare e pagare al prefato maestro Pietro o a suo figliolo in suo nome soldi diexedotto de quattrini per ogni centovinticinque para de carte, o vero triumphi para tanto manco de centovinticinque para, quanto gette el numero de le carte che ha più li iochi de li triumphi da quilli de le carte.
(Item that the aforesaid Mr. Roberto is obligated to give and pay to the aforesaid Master Pietro or his son in his name eighteen soldi of money for each 125 packs of cards, or true triumphs sufficiently less than for 125 packs, in so far as the number of the cards is more of Triumphs than of cards.)
As far as we know today, the common deck could have been formed of 40 cards, as Orioli affirms, but also by 32, 48, 52, or 56, and above all that of triumphs could have 60, again according to Orioli, or 62, as in the Bolognese Tarocchino, or 70, as in some testimonies of the time, or 78, as common subsequently in tarot cards, or even 96 if not 97, as in minchiate. Other numbers would have been possible for both decks.
In short, we can have fun in formulating the most varied possible combinations of the two numbers of cards, possibly through looking at pairs with a simple relationship between them, so as to facilitate the achievement of the final goal: to obtain whole numbers of packs, with the same total number of cards, producing both cards and triumphs.
However, by the end of the process, or even before starting it, we must ask a question in certain summary directions. Why in the contract itself is the numerical correspondence between cards and triumphs not very precisely expressed in an explicit manner? Even here I do not find only one sure answer, and thus I try to advance several hypotheses, so that the reader can choose the one that convinces him the most.
The simplest explanation I see is this: the card maker did not produce only cards or only triumphs, but in practice produced them together and on top of that in relatively variable amounts from time to time depending on demand or availability. Then there is no sense in making explicit the total number of decks of triumphs, because instead of 125 decks of cards he could have for example as numbers of decks (but not using these fictitious numbers for other accounts!) at one time 90 of cards and 30 of triumphs, another time 80 of cards and 35 of triumphs, and yet another, 70 of cards and 40 of triumphs, so that it would be
4
difficult to provide a list of all possible cases. Better to adjust the count [conte] from time to time.
Another possible explanation is that the two basic numbers were not fixed. The number of cards in the two decks could vary according to their destination. Out of place would be "my" Florentine numbers that could have been simply 48 and 96, which would still leave our schoolboy faced with an inconvenient result of 62.5 packs of triumphs instead of 125 of cards, the only safe number. However, other different compositions could have been produced to send to other cities.
The two proposed explanations so far are very different from each other, but share a common element: both suggest a possible reason not to write a second number in the contract, where in fact none appears.
However, anyone will be able to imagine a third easy solution: the number of cards in the common deck and in the triumphs was not only fixed, but also so well known to all that there was no need to write it explicitly in the contract, as evident to anyone reading it. We will try to go that route.
A key starting point for the search is as follows: if they produced both cards and triumphs there had to be a simple relationship between the two decks of cards, so that there were quite frequent coincidences in the total number of cards forming different numbers of related decks.
In other words, it would not be at all be convenient to produce from time to time cards in equal number, but corresponding to partial decks! If X decks of cards are produced together with Y decks of triumphs, the situation requires that X and Y be whole numbers; it is much better, the more they are found, these X and Y integers, for the same total number of cards.
Then the problem is no longer elementary school, even considering the existing uncertainty about the number of cards in their decks. But regardless of the cards of the two numbers in two different decks, it is from studying what the "comfortable" number of packs to produce is. We go to middle school and seek the possible X decks of cards and Y decks of triumphs.
The starting point is that X must be 125 if Y is zero. The total number of cards will be clearly XNc where I indicate with Nc the number, undetermined for now, of cards in the deck of regular cards. I indicate with Nt the number of cards in a deck of triumphs. Now we want the total number of cards to remain constant, albeit mixing decks of cards and triumphs.
This can be expressed simply as follows:

If Y = 0, that is, we produce only cards, X will be 125, as we knew from the start. But we can do the opposite, producing all triumphs and no decks of cards, that is, put X = 0. So once again we get a useful result:

But now we have put in addition the condition that Y must be an integer, because we do not want unuseful fractions of decks. We can then proceed by trial and error, using the most plausible values suggested above for both Nc and Nt, so as to verify what are able to be provided as Y integers.
One such attempt was made in the following table:
5
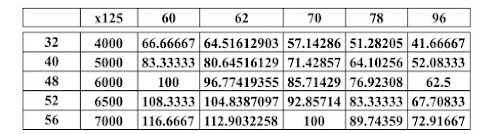
In the first column are "plausible" values of Nc' in the second these have been multiplied by "our" number of 125. Subsequent columns show the relationships 125 (Nc/Nt) for "plausible" Nt values as indicated on the top row.
We wanted Y to be an integer and in the table there are only two pairs of Nc and Nt that prove suitable. Unless introducing other plausible numbers of cards are introduced for the two decks, with those taken on a first attempt, there remain usable only 48/60 and 56/70.
In fact, it is precisely the starting number of 125 that is decisive for the entire procedure. Unfortunately for us, 125 is divisible only by 1 and 5; of the possible terms in n/5 with n an integer from 1 to 4, only 4/5 is a usable ratio in our case. So you find that to 125 decks of cards correspond 100 decks of triumphs.
In conclusion, it is found, by way of arithmetic, that triumphs were formed by the four usual suits of plus a fifth "suit" which had a number of cards equal to that of each of the four normal suits.
At this point we are ready to conclude the proceedings in the two directions taken. The first solution relates to the total numbers of decks that could be produced: the two extreme cases are clearly the 125 packs of only common cards, or, as we have now found, 100 packs of only triumphs.
All the possible intermediate cases for the numbers of mixed decks of cards and triumphs, including necessarily those in the range between 100 and 125, are listed in the following table and are numbers that increase one by one with the increase of the part of the common cards.

6
The second desired solution enters into the details of the cards contained in the two decks. The above table does not require precise numbers of cards in the two decks, but only that their relationship be of 4/5. Now we must examine which of the "plausible" numbers with 4/5 ratio are preferred.
In fact, the choice is rather limited, as shown in the following table:

From what we know so far, the choice of the number 70 for the deck of triumphs does not create particular problems. There are even historical documents in Ferrara which read precisely of decks of 70 cards for the trumps. Also Lothar Teikemeier has been advancing for years the proposal of a primitive deck of triumph cards of the format 5x14. (5)

Figura 1 – Schema of the two decks discussed.
7
The question, if need be, concerns the common deck of 56 cards, which cannot be said to be common. After all, the idea of a deck of 56 cards is not entirely unique, because it corresponds in particular to the "normal cards" present precisely inside the tarot decks known from later times, with the number cards from 1 to 10 and the upper four figures: page, knight, queen, king. Among other things, the presence of a pack like that seems already documented in the sermons of San Bernardino, where all four figures are mentioned.
To me, however, it remains difficult to imagine an Italian “common” pack of 56 cards used in "common" games. In Italy, of the four figures as a rule only three are used, choosing either the knight or the queen by region. Also of the ten numeral cards some are eliminated; more often, at least in the sequence, those from 8 to 10 inclusive.
The production of decks of 56 cards then would suggest that they were produced so as to meet the requirements of different locations, in which, if desired, the deck could be reduced in various ways to conform it to the games and to the habits of local players.
The proposed solution does not appear a hundred percent convincing. However, the possible alternatives convince even less, except perhaps that of 12 cards per suit, with a series of only 12 triumphal cards. In this second case, it would probably be easier to accept suits of 12 cards, but the triumphal series of only 12 cards would present itself as a bit too limited from what little we know. The remaining possibilities are even less convincing, although some elements in favor taken in particular cases can be found for almost all, including the ultimate of the deck of 80 cards.
In particular, I am convinced that the above is derived directly from the choice of the number 125 of groups of decks. I do not think that that number is compatible with other solutions based on randomly chosen numbers for the two decks: with any two numbers the numerical coincidence which leads to an equal total number of cards becomes exceptional for different quantities of complete decks of the two types.
Before, I thought that that strange 125 could be the result of a mistake in the transcription of the document; Now, I see rather clearly the technical reasons that had led to its choice.
Conclusion
A 1908 article was re-examined in which important Bolognese documents for the history of playing cards were published for the first time. Data in the documents have been commented on again, as well as the presence in Bologna of German card makers and in Florence of naibi in notarial acts.
On the basis of the number of 125 decks of cards indicated as a reference for production, some arithmetic exercises have been carried out, in order to define the numbers of cards present in decks of [common[ cards and also of triumphs in 1477 Bologna. The two most plausible corresponding numbers were 56 and 70.
Notes
1. Emilio Orioli, Il libro e la Stampa, II (1908), 109-119.
2. http://trionfi.com/0/e/00/
3. Lorenz Böninger, Die deutsche Einwanderung nach Florenz im Spätmittelalter. Leiden-Boston
2006.
4. http://naibi.net/A/64-ORPELLI-Z.pdf
5. http://trionfi.com/0/f/
Comments
(by Michael S. Howard; first posted on Tarot History Forum at http://forum.tarothistory.com/viewtopic.php?f=11&t=1128&p=18215&hilit=101#p18215)
Let us go back to the beginning of the “story problem”. The starting point is that X must be 125 if Y is zero. Franco says:
These are the first two steps. However it seems to me that he has skipped a step and also mislabled his first equation. That one is not about what happens when Y is zero. It is the equation that governs the contract, whatever X and Y may be. To get the result when Y is zero, we put Y=0 in the first equation, i.e.
XNc + (0)Nt = 125 Nc.
Which reduces to:
XNc = 125 Nc.
In other words, the total number of cards is 125 times the total number of decks, if there are no triumph decks. Using small “x” as multiplication, this could be written more explicitly (although visually confusing) as
X x Nc = 125 x Nc
This is a very small point, which really makes no difference and perhaps is more confusing than what Franco wrote, but I think it is important to be precise.
Then the next result
Y = 125 (Nc/Nt)
is correct, for what happens when X = 0. It gives a formula for calculating how many triumph decks will result when there are no common decks at all. It depends on the ratio of the number of cards per suit for common decks to the number of cards for triumph decks.
Then he plugs in numbers for Nt and Nc, picking out of the thousands of possibilities the most plausible ones he can think of, based on what little we know from the literature (Remember, for those of us used to a different convention, that the comma is a decimal point.)

To get these strange numbers, first he calculates how many cards there will be if Y equals zero, for different plausible numbers of cards in the common deck. In this case it does not matter how many cards there are in triumph decks, because Y = 0. The formula is X = Nc x 125. Various plausible amounts for Nc are in the first column, with the total number of cards in the second column.
Then, for the remaining columns, he calculates how many cards there will be if X equals zero, for various plausible numbers of cards in common and triumph decks, using the formula Y = 125 (Nc/Nt). He takes the result of multiplying 125 by Nc and dividing by the number Nt, for various plausible numbers of cards in triumph decks. There are only two cases where the result is an integer, meaning that there are no cards left over.
He could also have achieved the same result by first taking the ratio of Nc to Nt and then multiplying that by 125. In the case where Nt = 60 and Nc = 48, the ratio is 48/60. If we divide both the numerator and denominator by 12, it reduces to 4/5. In the case where Nt = 70 and Nc = 56, the result, dividing both numerator and denominator by 14, the result is also 4/5. Taking that times 125, we know that in each case there will be exactly 100 triumph decks.
The next table works out what happens if, holding the ratio of 4/5 constant, we increase the number of decks. Here are just the beginning and end of that table, all I need for the illustration.
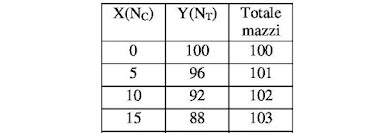

He finds that to get 101 decks, you have to increase the number of triumphs decks by 4, giving you 4 triumph decks and 95 common decks. It then proceeds in intervals of 4 until you arrive at 125 common decks as the maximum. The customer can get exactly a certain number of triumph decks vs. common decks only by picking a number of triumph decks divisible by 4, or a number of common decks divisible by 5.
His final step is to calculate the number of cards per deck given various numbers of cards per suit, between 8 and 16.

Not surprisingly, there are 4 times the cards per suit in common decks and 5 times in triumph decks. The ratio of 4/5 applies within the decks as well as between decks. The point is to show that the customer with this arrangement has considerable choice and flexibility in what decks to order, and how many cards per deck.
The only remaining issue that he goes into, briefly, is that it is not clear that the number of cards in a common deck is always the same, in practice, as the number of regular suit cards in the corresponding triumph deck. On that slightly disturbing note he ends the article. He has got what he wanted, a plausible number for triumph decks as implied by the contract reported by Orioli; this is because he thinks that 12 triumph cards per triumph deck or fewer is too low, based on what what little we know about the various tarot sequences, and that 14 is better. That 16 also works is some comfort, however, given what we know about the Cary-Yale.
Now I want to explain why I find Franco’s argument completely unconvincing. In essence, I see no reason using what happens when X = 0, i.e. there are only triumph decks, as a basis for what follows. The contractor is not asking for all triumph decks, but for a mixture of the two, and it happens that in such mixtures there are more possibilities for making the decks come out even than just that of a ratio 4/5 of cards in a common deck to cards in a triumph deck. However the result is either one that gives much less flexibility in the ratio of common decks to triumph decks that can be requested, or one that does not conform to the “plausible” numbers that Franco picked for his demonstration, based on what little we know. The operative word here is “little”, unfortunately. Also, Franco did not explore other plausible options, as he recognizes.
I will illustrate. Orioli had the suggestion of common decks with 40 cards and triumphs decks with 60. If so, that would be 20 cards particular to the tarot sequence. That is indeed a number that has been suggested for the tarot sequence: it could be the 22 minus the Tower and Devil cards, as we see in all the surviving PMB and PMB-clone cards, which, in the form we have them (i.e. with the 2nd artist cards), are probably of the same era as 1477 Bologna. Now it is easy to get numbers for triumph and common decks with such composition. We start with 125 common decks. If we change 3 of them to triumph decks, that will be 40 x 3 = 120 cards. For the same price we can have 2 truimph decks: 40 x 3 = 60 x 2. So with 122 common decks and 2 triumph decks, there are no cards left over. We can verify that with the formula that Franco gave at the beginning:
X Nc + Y Nt = 125 Nc
(122 x 40) + (2 x 60) = 125 x 40
4880 + 120 = 5000
Now our customer will probably want more than 2 triumph decks. Let us say that he sells three times as many common decks as he does triumph decks. If they had 40 cards, that would be around 31 of one and 94 of the other. But it is going to be fewer than 125 total, so fewer of each. We might guess 27 triumph decks. But that won’t work, because it isn’t divisible by 2. So let us guess 26. 26 triumph decks will take up 26x60 cards, equalling 1560. That equals 1560 divided by 40 common decks, i.e.. 39. Subtracting these 39 from 125 gives us 86 common decks and 26 triumph decks. 26 x 3 is 78, which isn’t enough triumph decks. 28 would give us 3 fewer common decks, i.e. 83. 28 x 3 = 84. So we go with 28 triumph decks and 83 common decks. Chccking our work:
28x60 + 83x40 = 125x40
1680 + 3320 = 5000
There is a formula our customer could have used, but to get it, one needs to know algebra, which I presume that our customer and card maker do not know. In that case, he is left with trial and error.
I will give another example that comes to the same thing. In Barcelona the composition of a regular deck around 1380 was given as 44 cards, according to Brunet y Bellet (viewtopic.php?f=11&t=1097&p=16954&hilit=Barcelona#p16954):
28x66 + 83x44 = 125x44
1848 + 3652 = 5500
It is also possible to order decks with any of the “plausible” combinations of common and triumph deck numbers in Franco’s first table. However there will be much less flexibility in quantities ordered. For example, for a 56 card common deck and a 78 card triumph deck, the ratio is 28 to 39. It will take 28 triumph decks to come out even. 28 triumph decks equals 39 common decks. So he will have to order 28, 56, or 84 triumph decks. If he orders 28 triumph decks, he will get 125-39 = 86 common decks, a ratio of close to 3 to 1.
For a 62 card triumph deck and 40 card common deck, the ratio is 31 to 20. The customer will have to order 20, 40, 60 or 80 triumph decks to come out even. With 20 triumph decks, he will get 125-39 = 86 common decks, a ratio of 4 to 1. With 40 triumph decks, he will get 125 - 78 = 47, close to even. 62 cards is not very flexible.
Another example is a 70 card triumph deck with a common deck of 48, as might be the case in Ferrara of 1457 (48 + 22). The ratio is 70 to 24. It will take 24 triumph decks to come out even; so our customer again does not have very many choices.
It is even possible to order 96 card triumph decks (assuming 56 cards in the common deck). The ratio is 96/56 = 12/7. He can order 7, 14, 21, 28, etc. triumph decks Let us try 28. 28 triumph decks uses up 28x96/56 = 48 common packs’ worth of cards, leaving 125 – 48 = 77 common decks. Well, that’s the best we can do. 21 would give 125 – (21x96/56) = 125 – 36 = 89, which is far more than 3 to 1.
A 97 card triumph deck is very inconvenient. The ratio is 97/56. It would take 56 triumph decks to make it come out even. 125 – 97 = 28 common decks. The customer would have to buy 97 triumph decks and 28 common decks.
97x56 + 28x56 = 125x56
At the end Franco brings up the issue that the common decks might not be simply the triumph decks minus the special triumph cards. That is no problem; the math works the same. Let us say that there are 48 card common decks and 96 card triumph decks (as might be the case for the Rosenwald). The ratio is 1/2, by far the most favorable yet. You can order any number of triumph decks you like (as long as you don't go over 48x125 cards total), and the result will come out even. Let us try 24 triumph decks. Then there are 125 – (24x96/48) = 77 common decks. That is close. But 25 triumph decks would be 125 – (25x96/48) = 75. That is exactly what we wanted.
In conclusion, almost anything works, given Arioli’s figures, depending on how flexible you can be. The lower the number in numerator of the ratio of common decks and triumph decks, the more flexible you can be. The ratio of 4 to 5 is not bad, and if the customer wants to make nothing but triumph decks, but for some reason expressed in a contract that is in terms of common decks and precisely 125 of them, it would be the best. But for mixed orders, common and triumph decks, a ratio of 2 to 3 is even better. Making for much less flexibility are both a 62 and a 78 card triumph deck. Thus Orioli's numbers of 40 and 60 are plausible. 48 and 96 offer the most flexibility of all, but I would have expected the word "minchiate" or "germini" to be used. I am left wondering if the tarocchino deck might not have originally been 66 cards, in which case a 22 card tarot sequence with 11 cards per regular suit.
(by Michael S. Howard; first posted on Tarot History Forum at http://forum.tarothistory.com/viewtopic.php?f=11&t=1128&p=18215&hilit=101#p18215)
Let us go back to the beginning of the “story problem”. The starting point is that X must be 125 if Y is zero. Franco says:
The total number of cards will be clearly XNc where I indicate with Nc the number, undetermined for now, of cards in the deck of regular cards. I indicate with Nt the number of cards in a deck of triumphs. Now we want the total number of cards to remain constant, albeit mixing decks of cards and triumphs.
This can be expressed simply as follows:
If Y = 0, that is, we only produce cards, X will be 125, as we knew from the start. But we can do the opposite, producing all triumphs and no deck of cards, that is, put an X = 0. So once again you get a useful result:

These are the first two steps. However it seems to me that he has skipped a step and also mislabled his first equation. That one is not about what happens when Y is zero. It is the equation that governs the contract, whatever X and Y may be. To get the result when Y is zero, we put Y=0 in the first equation, i.e.
XNc + (0)Nt = 125 Nc.
Which reduces to:
XNc = 125 Nc.
In other words, the total number of cards is 125 times the total number of decks, if there are no triumph decks. Using small “x” as multiplication, this could be written more explicitly (although visually confusing) as
X x Nc = 125 x Nc
This is a very small point, which really makes no difference and perhaps is more confusing than what Franco wrote, but I think it is important to be precise.
Then the next result
Y = 125 (Nc/Nt)
is correct, for what happens when X = 0. It gives a formula for calculating how many triumph decks will result when there are no common decks at all. It depends on the ratio of the number of cards per suit for common decks to the number of cards for triumph decks.
Then he plugs in numbers for Nt and Nc, picking out of the thousands of possibilities the most plausible ones he can think of, based on what little we know from the literature (Remember, for those of us used to a different convention, that the comma is a decimal point.)

To get these strange numbers, first he calculates how many cards there will be if Y equals zero, for different plausible numbers of cards in the common deck. In this case it does not matter how many cards there are in triumph decks, because Y = 0. The formula is X = Nc x 125. Various plausible amounts for Nc are in the first column, with the total number of cards in the second column.
Then, for the remaining columns, he calculates how many cards there will be if X equals zero, for various plausible numbers of cards in common and triumph decks, using the formula Y = 125 (Nc/Nt). He takes the result of multiplying 125 by Nc and dividing by the number Nt, for various plausible numbers of cards in triumph decks. There are only two cases where the result is an integer, meaning that there are no cards left over.
He could also have achieved the same result by first taking the ratio of Nc to Nt and then multiplying that by 125. In the case where Nt = 60 and Nc = 48, the ratio is 48/60. If we divide both the numerator and denominator by 12, it reduces to 4/5. In the case where Nt = 70 and Nc = 56, the result, dividing both numerator and denominator by 14, the result is also 4/5. Taking that times 125, we know that in each case there will be exactly 100 triumph decks.
The next table works out what happens if, holding the ratio of 4/5 constant, we increase the number of decks. Here are just the beginning and end of that table, all I need for the illustration.


He finds that to get 101 decks, you have to increase the number of triumphs decks by 4, giving you 4 triumph decks and 95 common decks. It then proceeds in intervals of 4 until you arrive at 125 common decks as the maximum. The customer can get exactly a certain number of triumph decks vs. common decks only by picking a number of triumph decks divisible by 4, or a number of common decks divisible by 5.
His final step is to calculate the number of cards per deck given various numbers of cards per suit, between 8 and 16.

Not surprisingly, there are 4 times the cards per suit in common decks and 5 times in triumph decks. The ratio of 4/5 applies within the decks as well as between decks. The point is to show that the customer with this arrangement has considerable choice and flexibility in what decks to order, and how many cards per deck.
The only remaining issue that he goes into, briefly, is that it is not clear that the number of cards in a common deck is always the same, in practice, as the number of regular suit cards in the corresponding triumph deck. On that slightly disturbing note he ends the article. He has got what he wanted, a plausible number for triumph decks as implied by the contract reported by Orioli; this is because he thinks that 12 triumph cards per triumph deck or fewer is too low, based on what what little we know about the various tarot sequences, and that 14 is better. That 16 also works is some comfort, however, given what we know about the Cary-Yale.
Now I want to explain why I find Franco’s argument completely unconvincing. In essence, I see no reason using what happens when X = 0, i.e. there are only triumph decks, as a basis for what follows. The contractor is not asking for all triumph decks, but for a mixture of the two, and it happens that in such mixtures there are more possibilities for making the decks come out even than just that of a ratio 4/5 of cards in a common deck to cards in a triumph deck. However the result is either one that gives much less flexibility in the ratio of common decks to triumph decks that can be requested, or one that does not conform to the “plausible” numbers that Franco picked for his demonstration, based on what little we know. The operative word here is “little”, unfortunately. Also, Franco did not explore other plausible options, as he recognizes.
I will illustrate. Orioli had the suggestion of common decks with 40 cards and triumphs decks with 60. If so, that would be 20 cards particular to the tarot sequence. That is indeed a number that has been suggested for the tarot sequence: it could be the 22 minus the Tower and Devil cards, as we see in all the surviving PMB and PMB-clone cards, which, in the form we have them (i.e. with the 2nd artist cards), are probably of the same era as 1477 Bologna. Now it is easy to get numbers for triumph and common decks with such composition. We start with 125 common decks. If we change 3 of them to triumph decks, that will be 40 x 3 = 120 cards. For the same price we can have 2 truimph decks: 40 x 3 = 60 x 2. So with 122 common decks and 2 triumph decks, there are no cards left over. We can verify that with the formula that Franco gave at the beginning:
X Nc + Y Nt = 125 Nc
(122 x 40) + (2 x 60) = 125 x 40
4880 + 120 = 5000
Now our customer will probably want more than 2 triumph decks. Let us say that he sells three times as many common decks as he does triumph decks. If they had 40 cards, that would be around 31 of one and 94 of the other. But it is going to be fewer than 125 total, so fewer of each. We might guess 27 triumph decks. But that won’t work, because it isn’t divisible by 2. So let us guess 26. 26 triumph decks will take up 26x60 cards, equalling 1560. That equals 1560 divided by 40 common decks, i.e.. 39. Subtracting these 39 from 125 gives us 86 common decks and 26 triumph decks. 26 x 3 is 78, which isn’t enough triumph decks. 28 would give us 3 fewer common decks, i.e. 83. 28 x 3 = 84. So we go with 28 triumph decks and 83 common decks. Chccking our work:
28x60 + 83x40 = 125x40
1680 + 3320 = 5000
There is a formula our customer could have used, but to get it, one needs to know algebra, which I presume that our customer and card maker do not know. In that case, he is left with trial and error.
I will give another example that comes to the same thing. In Barcelona the composition of a regular deck around 1380 was given as 44 cards, according to Brunet y Bellet (viewtopic.php?f=11&t=1097&p=16954&hilit=Barcelona#p16954):
If that number was maintained in Bologna, and 22 more card were added to make a triumph decks, the ratio would be 44/66. That reduces to 2/3 and will have just as many possibilities for coming out even as the previous example. Again, a customer can get his 3 to 1 ratio by ordering 83 common decks and 28 triumph decks.En 1’inventari de Nicoláu Sarmona, negociant de Barcelona, carrer de S. Daniel, any 1380 va continuat un «Ludus de naips qui sunt 44 pecie.
28x66 + 83x44 = 125x44
1848 + 3652 = 5500
It is also possible to order decks with any of the “plausible” combinations of common and triumph deck numbers in Franco’s first table. However there will be much less flexibility in quantities ordered. For example, for a 56 card common deck and a 78 card triumph deck, the ratio is 28 to 39. It will take 28 triumph decks to come out even. 28 triumph decks equals 39 common decks. So he will have to order 28, 56, or 84 triumph decks. If he orders 28 triumph decks, he will get 125-39 = 86 common decks, a ratio of close to 3 to 1.
For a 62 card triumph deck and 40 card common deck, the ratio is 31 to 20. The customer will have to order 20, 40, 60 or 80 triumph decks to come out even. With 20 triumph decks, he will get 125-39 = 86 common decks, a ratio of 4 to 1. With 40 triumph decks, he will get 125 - 78 = 47, close to even. 62 cards is not very flexible.
Another example is a 70 card triumph deck with a common deck of 48, as might be the case in Ferrara of 1457 (48 + 22). The ratio is 70 to 24. It will take 24 triumph decks to come out even; so our customer again does not have very many choices.
It is even possible to order 96 card triumph decks (assuming 56 cards in the common deck). The ratio is 96/56 = 12/7. He can order 7, 14, 21, 28, etc. triumph decks Let us try 28. 28 triumph decks uses up 28x96/56 = 48 common packs’ worth of cards, leaving 125 – 48 = 77 common decks. Well, that’s the best we can do. 21 would give 125 – (21x96/56) = 125 – 36 = 89, which is far more than 3 to 1.
A 97 card triumph deck is very inconvenient. The ratio is 97/56. It would take 56 triumph decks to make it come out even. 125 – 97 = 28 common decks. The customer would have to buy 97 triumph decks and 28 common decks.
97x56 + 28x56 = 125x56
At the end Franco brings up the issue that the common decks might not be simply the triumph decks minus the special triumph cards. That is no problem; the math works the same. Let us say that there are 48 card common decks and 96 card triumph decks (as might be the case for the Rosenwald). The ratio is 1/2, by far the most favorable yet. You can order any number of triumph decks you like (as long as you don't go over 48x125 cards total), and the result will come out even. Let us try 24 triumph decks. Then there are 125 – (24x96/48) = 77 common decks. That is close. But 25 triumph decks would be 125 – (25x96/48) = 75. That is exactly what we wanted.
In conclusion, almost anything works, given Arioli’s figures, depending on how flexible you can be. The lower the number in numerator of the ratio of common decks and triumph decks, the more flexible you can be. The ratio of 4 to 5 is not bad, and if the customer wants to make nothing but triumph decks, but for some reason expressed in a contract that is in terms of common decks and precisely 125 of them, it would be the best. But for mixed orders, common and triumph decks, a ratio of 2 to 3 is even better. Making for much less flexibility are both a 62 and a 78 card triumph deck. Thus Orioli's numbers of 40 and 60 are plausible. 48 and 96 offer the most flexibility of all, but I would have expected the word "minchiate" or "germini" to be used. I am left wondering if the tarocchino deck might not have originally been 66 cards, in which case a 22 card tarot sequence with 11 cards per regular suit.
Additional comments (originally posted Dec. 4, 2016, at http://forum.tarothistory.com/viewtopic.php?f=11&t=1092&start=30#p18280):
Franco emailed me that he would like to know if from my perspective I
could produce tables similar to the ones he produced, i.e. the one that
had 0-100-100 on top and 125-0-125 on the bottom, except for different
ratios of common decks to triumph decks. I thought that was a good idea,
if only to double check the soundness of the argument. I have produced 4
such tables, for 4 different ratios, 2 at opposite ends of the spectrum
and 2 in the middle. That should be sufficient to show that in every
case, up to the limit of 125Nc total cards, it will be possible to
construct such a table. Of course there will be, in all my examples,
one row of the table blank, namely the case where only triumph decks are
produced. But this was a case explicitly excluded from the contract.
First, for Orioli's 40 common cards, 60 triumphs example:
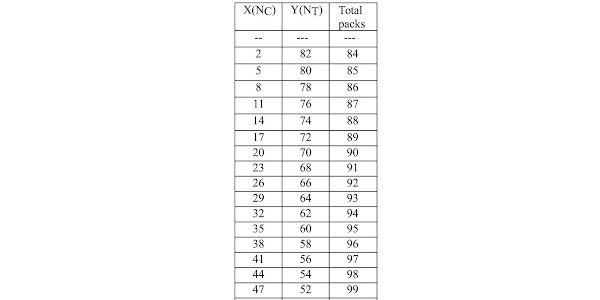



If you count them, you will find that there are 41 choices, plus the choice of all common decks, as opposed to 26 in the case of the 4/5 ratio. This will be the same for any 2/3 ratio deck. And this is not the ratio that gives the maximum number of choices. For 48/96 ratio decks, and anything with a ratio of 1/2, there will be 63 choices, i.e. one more than half the number of common decks. The final choice will be 62 triumph decks plus 1 common deck. That doesn't include the choice of all common decks, so with that one there will be 63 choices.
Now for my second example, at the other extreme, a 97 card triumph deck with a 56 card common deck. so a 56/97 ratio.



If the customer wants more common decks to go with his 56 triumph decks, he will have to order 125 of them for a double order, for a total of 56 triumph decks and 153 common decks.
My third example is the 62 card triumph deck along with 40 card common decks. His choices are below:



These are not very many choices, but at least there is more than one, and they offer come variety.
A 78 card triumph, 40 to 56 card common deck will offer similar choices, except with the 48 card common deck, which will offer two or thee times more. For 48 common card decks, the ratio will be 8/13, vs. 20, 22, 26, or 28 over 39 for the others; it is the numerator that is decisive, while the denominator affects how low the numerator can be. Here are the choices for 78 triumph and 48 common card decks.


There are 10 choices, as opposed to 4 with the 40 card common pack, or 9 and 3 without the all-common card decks choice. That is not 41 or 42, but it is better than 3 or 4.
First, for Orioli's 40 common cards, 60 triumphs example:




If you count them, you will find that there are 41 choices, plus the choice of all common decks, as opposed to 26 in the case of the 4/5 ratio. This will be the same for any 2/3 ratio deck. And this is not the ratio that gives the maximum number of choices. For 48/96 ratio decks, and anything with a ratio of 1/2, there will be 63 choices, i.e. one more than half the number of common decks. The final choice will be 62 triumph decks plus 1 common deck. That doesn't include the choice of all common decks, so with that one there will be 63 choices.
Now for my second example, at the other extreme, a 97 card triumph deck with a 56 card common deck. so a 56/97 ratio.



If the customer wants more common decks to go with his 56 triumph decks, he will have to order 125 of them for a double order, for a total of 56 triumph decks and 153 common decks.
My third example is the 62 card triumph deck along with 40 card common decks. His choices are below:



These are not very many choices, but at least there is more than one, and they offer come variety.
A 78 card triumph, 40 to 56 card common deck will offer similar choices, except with the 48 card common deck, which will offer two or thee times more. For 48 common card decks, the ratio will be 8/13, vs. 20, 22, 26, or 28 over 39 for the others; it is the numerator that is decisive, while the denominator affects how low the numerator can be. Here are the choices for 78 triumph and 48 common card decks.


There are 10 choices, as opposed to 4 with the 40 card common pack, or 9 and 3 without the all-common card decks choice. That is not 41 or 42, but it is better than 3 or 4.
Appendix: Translation of Orioli's comments on the contract and a rough translation of the contract itself
Emilio Orioli, excerpt from "Sulle carte da giuoco a Bologna nel secolo XV", Il libro e la stampa n.s. 2, fasc. 4-5 (1908), pp. 109-119, this part pp. 113-114. For a transcription of the Italian, see Ross Caldwell at http://trionfi.com/0/e/35. This translation originally posted Dec. 5, 2016 at http://forum.tarothistory.com/viewtopic.php?f=11&t=1128#p18253.
And now for the contract itself, starting with the original (from the photocopy at http://trionfi.com/0/e/35/), paragraph by paragraph, numbered, each paragraph followed by my translation, interrupted occasionally with my commentary on the wording and my impression of what is being said. For the translation, I tried to think of alternate spellings for words I couldn't find and also looked in Florio's 1611 Italian-English dictionary in such cases. I think it is fairly intelligible except the last sentence of the contract. Comments in brackets are mine; frequently they are to give the modern word that I assume corresponds to the spelling in the contract. I left the honorific "ser" as in the original, as the meaning does not quite have a modern equivalent; it does not imply knighthood, but it is more honorific than either the English "Mr.", or "sir" as said to a presumed superior. I decided that "o vero", which I translated as "or true", probably is just an old way of saying "ovvero", which means the same as "o" by itself, i.e. "or".(first posted Dec. 6, 2016, at http://forum.tarothistory.com/viewtopic.php?f=11&t=1128&start=10#p18262; before and after that post, there is interesting discussion of the raw materials referred to and their cost).But back to the cards of the hand-painted game. Worthy of note is a contract concluded in 1477 by the notary Alberto Argellata between a Roberto Blanchelli of Rimini, residing in Bologna, who was the client, with master Pietro Bonozzi, dealer of the elders, who is obliged with certain pacts concerning "the craft of playing cards and triumphs"; which pacts had to be fulfilled by his son, toward whom Blanchelli undertook to provide him with a certain quantity of playing cards of two different species. This contract, besides the agreed price, also established the way the cards were to be processed, according to a model [modello] prepared and kept by a third person; that if they were not identical or proved to be executed badly, Pietro Bonozzi was obliged to do them over; they should not have any design on the back but be perfectly white. It obliged also said Master Pietro not to let his son or any other to work on or sell their cards to others, except for Blanchelli, or help or counsel others around said craft much less teach it to others; instead he promised that in the space of eighteen continuous months he would devote himself to preparing cards and triumphs solely on behalf of Blanchelli; who in turn, he had to provide the paper and cardboard [cartoni] needed to make "said cards or true Triumphs". Besides the agreed upon reward Blanchelli had also to add eighteen soldi designated for expenses, for each hundred and twenty-five decks of cards or likewise packs of corresponding true triumphs, but taking into account the greater number of pieces needed for forming a pack, because "Triumphs has more of them than those of cards". Now to explain this passage, we must bear in mind the distinction that is always made in this act, between "cards" and "triumphs." The word "cards" means the usual pack of cards, formed of forty pieces; instead the word "triumph", which also is seen mentioned in the document of 1459, is to signify the "Bolognese tarot", i.e. the so-called "long” cards, of which we know that it takes sixty to form the deck. For expenditures therefore must be taken account not packs, but number of cards that it actually takes to form them; the eighteen soldi that Blanchelli is obliged to pay in addition, by way of expenses, were then to be used to purchase "verzino, vederamo, agiuro, glue, alum de roza, ink to make said cards or Triumphs".
In nomine Domini amen Rogiti di Alberto Argelatta, Filza 4a, n. 113
1. Questi sono certi patti a conventione le quali ser Roberto Blanchelli di Arimino habitador in Bologna in la capella s. Maria del Tempio e maestro Pietro Bonozo maziero de li nostri magnifici Signori e conservadori de Bologna hanno facto inseime sopra el mestiero de la carte e triumphi da zugare, le quale esso ser Roberto fa fare al figliolo del dicto maestro Piero Bonozo con li capituli e conventione infrascripte; zoe e primo. Chel dicto maestro Piero sia obligato fare e operare che el prefato suo figliolo durante el tempo e termine de sei misi proximi che viranno, incomenzando dal di soprascripto finendo como segue, fara al prefato ser Roberto per zascuno mese almanco para de carte da giugare doxento cinquanta ben lavorate ben netto ben coperte a custodite ad arbitrio de beno homo, segondo che sera la prima mostra che lui glie dara la quale se debia observare apresso d’uno terzo e debiano esser tutte a similitudine di quella, de la quale 250 para sia tenuto darne omne volta para 50 stenchite de fuora e alcune con le arme segondo la volonta di esso maestro Piero tutte bianche de fuora. E cosi facte le debia tutte consignare a esso Roberto o tutte insieme o a parte a parte secondo la volontà di Roberto.
You can see here that Pietro is already of some note, being card-maker to the Signoria of the cit of Bologna.In the name of God, amen, Requested of Alberto Argelatta, File 4a, no. 113
1. These are certain pacts of agreement, which ser Roberto Blanchelli of Arimino living in Bologna in the parish of S. Maria of the Temple and master Pietro de Bonozo craftsman to our magnificent Signori and the conservators of Bologna have made together on the craft of cards and triumphs for playing, which this ser Roberto makes to the son of said master Piero Bonozo with the sections [capitoli]] and agreement made below; zoe [?] and first. That said master Piero is obligated to operate and work so that the aforesaid son during the time and term of six months [mesi] next [prossimi] beginning [che varano], beginning from above ending as follows, will make the aforesaid ser Roberto for some [alcuno?] month at least [almeno] two hundred fifty packs of playing cards well worked well very clean, well protected in custody at the will of a good man, according [secondo] that he at the first showing that he gives must be observed afterwards [appresso] by a third [person] and must all be in the likeness of that, of which 250 packs are kept to give every time 50 packs dried [stenchite = stecchite? or perhaps something etymologically related to "stenciled"] outside and some with arms according to [secondo] the will of this master Piero, all of them white outside. So done he must consign all for Roberto, either all together, or apart according to the will of Roberto.
I have no idea what "zoe e primo" means. "Zio" is "uncle", so it might be "uncle and cousin". A "son" is not necessarily a blood relative, but could just be an apprentice, I remember reading somewhere.
The words "zascuno mese" are both in the singular, yet the context would seem to imply not "any month" (much less "every month") but rather, "any months", as it is speaking about the first 250 common packs' worth of cards. Oddly our notary has the plural of "mese" as "misi", as though two i's were better than one.
I tried to trace "stencil" back to 15th century Italian but have not been successful. The only 15th century meaning that the Oxford English Dictionary has is as a verb, meaning "To ornament with bright colours or pieces of precious metal", a meaning now obsolete. It derives from the Old French estanceler, estenceler, and the popular Latin "stincilla metathesis of scintilla spark". "Stincilla" (noun) is perhaps not far from "stenchite" (participle). The 1420 English example, "stanseld" (i.e. "stenciled"), is from an Arthurian romance, describing the attire of a knight and his horse. The Middle English noun meaning the same, the ornamentation, is stansel. With the modern meaning, its first use is 1707, describing precisely the making of playing cards. No additional explanation of how the word got applied to that context, but I presume it was because bright colors were added as ornamentation. "Stecchita", meaning "dried up", also fits the context. Andrea Vitali has an essay transcribing an 18th century article on card-making, http://www.associazioneletarot.it/page.aspx?id=228. The modern word he uses for the stencil (there is even a picture) is "Mascherina", but with the word "trasforo" in parentheses, which is the word used in the document.
Checking my transcription of the contract, I see that earlier I misread "volta" as "volia". "Volta" is much better. I continue:
I am not sure what the provisions here are. The first line seems to imply that Roberto will provide the "forme", some sort of template, whether of wood or cardboard is unclear to me. The last part seems to give Roberto the option of releasing Piero and his son from the obligation after 6 months, but otherwise 18 months; the decision seems to be up to Roberto.2. Item che se qualche volta esso Roberto volesse che lui glie fesse fare di triumphi che alhora el prefato maestro Piero sia obligato fargliene fare nel modo proprio che le obligato a le carte ma a rasone de carta per carta debia essere pagato come de la carte e non piu.
(Item that if sometimes it Roberto wants them to make triumphs, that then the aforesaid master Piero is obligated to make them in the proper way, but rightfully paid card by card and not more.)
3. Item che quando li glie fesse fare o carte o triumphi che non stessero bene a fussero mal facti chel sia obligato farglieli refare a tutte sue spese.
(Item, that when they make cards or triumphs that are not good and are poorly made that he is obligated to redo them at all his own expense.)
4. Item chel prefato maestro Piero sia obligato fare e operare si che ne el prefato suo figliolo ne alcuno di suoi o altri con suo conscentimento non lavoranno ne faranno lavorare ne daranno ad altri ne adiuto ne consiglio de dicto mestiere de carte o triumphi ne le venderanno o faranno vendere ne insigneranno el mestieri ad altri sotto pena di L. cinque de bolognini, ne le quale sia obligato de rato e sia licito ad esso ser Roberto retenergliele omne volte e tante volte quante lui glie podesse provare che lui o alcuno di suoi fessero o consentessero alcuna de le predicte de le salarii che esso ser prefato ser Roberto le sera obligato per li lavori le fara suo figliuolo, comuno di sotto appare.
(4. Item, that the aforesaid master Piero is obligated to do and work that the aforesaid his son nor any of his or other with his consent will work nor give work to others with advice or counsel of said expertise of cards or triumphs nor sell or arrange that others sell nor consign the craft to others, under penalty of five Lire bolognini, to whom it is obligated to be confirmed and lawful to this ser Roberto to retain it from them every time and as many times as he can prove that he or any of his made or consigned any of the of the aforesaid from the salaried [salarati] that this aforesaid ser Roberto obligated as work to be done by his son, as appears below.)
5. Item cbe [misprint for "che"?] el prefato ser Robert sia obligato durante el tempo di prefati sei misi mantenere el prefato figliolo de maestro Piero in continno lavoriero in forma che mai non li manchi de fare, maximamente per insino a la somma de le carte sopra scripte per zascmio mese e anco de cento vinticinque para de piu se tante ne potra o vora fare, con pacto che se do co di sei mesi el prefato ser Roberto volesse desitere de simile imprese che lui la possa lassare e che ognuno sia in sujo aritrio, ma quando lui volesse andare ‘drieto che allora il prefato Piero sia obligato perseverare e fare perseverare suo figliolo nel prefato mestiere altri dodexe misi con li pacti medesimi che in questa scripta se contengono, reservato sempre a Roberto che se de co de omne sei misi per insino al spatio de dexedotto misi volesse lassare stare tale impresa che lui la pessa lassare stare segondo la soa volonta e passati li diexedotto misi ognuno sia in suo arbitrio: e questo pacto sia obligato servare l’una e l’altra parte sotto pena de ducati diexe ne la quale de facto incorra chi contrafara a le predicte cose la quale pena sia de colui che stara perseverante a quanto di sopra.
(Item, that ser aforesaid Roberto is obligated during the time of the six months to keep the aforesaid son of master Piero in continuous working in form [already incised woodblocks?] that he never lack for making, for maximally so far [infino] to the sum of the cards as written above for any month likewise of 125 packs, more if he can or will make them, with pact to make that if with six months aforesaid ser Roberto wanted to discontinue similar business that he can grow weary [lassare, or lascare = loosen?] and everyone is at his will, but when he wanted go ahead [adietro] then the aforesaid Piero is obligated to persevere and make his son persevere in the aforesaid trade with another 12 months with the same pact that is contained in this writing, always reserved to Roberto that if with all six months so far in the space of 18 months he wanted to grow weary [lassare] of that endeavor he could become weary of [lassare] it according to his will and pass the 18 months each one to his will: and in this pact it is obligated to preserve the one and the other part on pain of ten ducats which he in fact incurs who contravenes the aforesaid things, which penalty is with the one perseverant to the above.
7 and 8 are where the puzzling word "cartuni", the modern "cartoni", first appears. It could mean cartoons, cardstock, cardboard, or cartons, i.e. boxes. In 1507 Florence, according to Franco in another article, the word "cartoni" meant "cartons," he told me. But it seems clear that in the 18th century document that Andrea transcribed it meant "cardstock", that is, a sheet of uncut cards. However I cannot translate that document very well either. In this case it could be any of the various possibilities, even cartoons, in the sense of preliminary drawings or possibly even stencils.6. Item che el prefato maestro Piero sia obligato consgnare al dicto ser Roberto tutti li retagli che vi siranno de dicte carte.
(6. Item, that aforesaid maestro Piero is obligated to consign to the said ser Roberto the cuttings [or remainders: ritagli] all that there will be from said cards.)
7. Item chel prefato ser Roberto sia obligato dare al prefato maestro Piero o a suo figliolo predicto tutte le carte e cartuni che andaranno per fare dicte carte o vero triumphi secondo el consueto e segondo quello che se le fara overo dira qualunche altro maestro de simile misterio a tutte sue proprie spese.
(7. Item that the aforesaid ser Roberto is obligated to give the aforesaid master Piero or his aforesaid son all the paper and cartons [cartoni] that go to make said cards or triumphs according the usual and according to what some other master of similar craft will do or say, to all his own expense.)
8.Item che el prefato ser Roberto sia obligato dare e pagare al prefato maestro Piero o a suo filiolo in sao nome soldi diesedotto de quattrini per ogni centovincinque para de carte, o vero triumphi para tanto manco de centovinticinque para, quanto gette el numero de la carte che he piu li jochi de li triumphi da quilli de le carte. E quisti soldi diexedotto sonno per vergino, verderamo, agiurro, colla, ove, alum de roza inchiostro per colori e generalmente per ogne altre spese che podesse andare in fare dicte carte o triumphi, li quali decedotto soldi pagati a prefato maestro Piero sia obligato farle poi li fare a tutte sue spese de le carte e cartuni infuore le quale esso ser Roberto glie debia dare e pagare como di sopra.
(8. Item: that aforesaid ser Roberto is obligated to give and pay the aforesaid Piero master or his son in his name 18 soldi of money for each 125 packs of cards, or triumph packs of less than 125 packs, no matter if the number of cards is more for playing cards or triumphs. And this 18 soldi is for vergino, verderamo, agiurro, glue, eggs [uova], alum de roze for ink coloring and generally for all other expenses that could go into making said cards or Triumphs, 18 soldi paid to aforesaid master Piero is obligated to make then at his own expense the cards and exterior cartons [cartuni infuore] which this ser Roberto must give and pay him as above.)
SteveM has done a good job identifying verdino, alum de roza, verderamo, and aguirro to the extent possible (viewtopic.php?f=11&t=1128&start=10#p18257, viewtopic.php?f=11&t=1128&start=10#p18260). The latter two would indeed seem expensive. Perhaps he doesn't use much. He wrote"
verzino, vederamo, agiuro, colla, alume de roza, inchiostro per fare dicte carte o triumphi" = "brazilwood (to make reds), verdigris (to make greens), azure (to make blues), glue, potash (a mordant, colour fixative), ink to make said cards or triumphs".
And now for the last paragraph of the contract. I still have not made much sense of the last sentence. Any help would be appreciated:
My only guess, for the last sentence, is that even after the agreement is satisfied, if Roberto needs more packs, the price of 5 lire per 125 common packs' worth still holds. But this is just a wild guess.9. Item chel prefato ser Roberto sia obligato dare e pagare el prefato maestro Piero overo a so figlilo, piacendo a lui, per ogni cento vinticinque para de carte che lui glie fara fare, o vero triumphi, a rata per rata del numero de le carte como di sopra Lire cinque de bolognini de moneta corente e quisti per la sua fatica e mistiero che durara dicto suo figliolo in farli fare dicte carte e triumphi; cum pacto che el prefato maestro Piero non possa ne debia mai domandare alcuno dinaro de la mercede del figliolo al prefato ser Roberto se non de co de omne mese. El quale finito alhora dicto ser Roberto sia obligato fare rasone con lui e debia infra termine de octo di seguenti in mediate depoi dicto mese finito pagarlo interamente de tutto quello che al prefato suo figliolo glie haveva francato a la rasone pacti e conventione soprascripti, o vero sia licito a esso ser Roberto sempre durante el tempo di questa conventione retenerse in mano Lire cinque de quattrini de quelle se havera francate a lavorare el dicto figliolo de maestro Piero e de le altre che lui se francara sia obligato pagarlo sempre de volta in volta, segondo che lui glie consignara el lavoriero e sia licito al dicto maestro Piero de quisti dui ultimi partioli pigliare quale glie piace.
Item that aforesaid ser Roberto is obligated to give and pay aforesaid master Piero or his son, if it pleases him, for every 125 packs of cards or Triumphs that he will make payment, according to the number of cards as above, five bolognini Lire of current money and this for his effort and expertise of his said son in making said cards and Triumphs; with the pact the aforesaid master Piero cannot ever ask any money of award of the son to the aforesaid ser Roberto if not of that every month. The which finshed then said ser Roberto is obligated to do right with him and must below finish of eight [otto?] following by intercession since said month finished pay him fully all that the aforesaid son had released by right of the pacts and agreement written above or is lawful to ser Roberto still during the time of this agreement to retain in hand five Lire of money of what has been released to work said son of master Piero and of the others if he will release be obligated to pay still from time to time, according to the work and it is lawful to said master Piero from these last two parts to take what pleases him.
Then there are the signatures:
Io Roberto soprascripto scripse de mia mano propria.
Io Piero de Iacomo Bonozo sopra scrito fo paio convencion e obligazion con el dito ser Ruberto e si me obligo prinzipalemente soto la pena che si contiene in lo instromento rogado per man de ser Alberto d’Argela nodaro.
Io Piero Bonozo de mia man propria scrise.
(I above written Roberto written of my own hand.
I Piero de Jacomo Bonozo above written the [?] pair agreement and obligazion with the said ser Ruberto and oblige myself principally under penalty that is contained in the instrument requested by hand of ser Alberto d'Argela notary.
I Piero de Bonozo of my own hand written.)
No comments:
Post a Comment